Varbūtiskā loģika. Pamatprincipi
A
Varbūtiskajā
loģikā mūsu slēdzieni saistīti ar spriedumiem, kuros
atklāti vai apslēpti figurē varbūtības termins.
Šāda tipa sprieduma piemērs ir apgalvojums, ka spēļu
kauliņa noteiktas skaldnes uzkrišanas varbūtība ir 1/6.
Šai kategorijai pieder arī apgalvojums varbūtība, ka
jaunas ģimenes pirmdzimtais būs zēns ir ½.
Svarīgi atzīmēt, ka
pastāv būtiska atšķirība starp varbūtības
jēdziena saturu, ar kuru operējam sadzīvē, un šī
termina semantiku tehnikā un dabas zinātnēs. Pirmajā
gadījumā mums ir darīšana ar t. s. subjektīvo
varbūtību, otrajā - ar objektīvo. Zēna vai meitenes
piedzimšana pieskaitāma objektīvo varbūtību
kategorijai un interpretējama kā attiecīgās
parādības novērojamais biežums samērā lielā
izmēģinājuma skaitā. Tā, piemēram, ja uz labu
laimi izvēlēsimies tūkstoš ģimeņu, tad zēnu
un meiteņu skaita attiecība pirmdzimto vidū būs ļoti
tuva 500/500. Pavisam citu statistisko biežumu iegūsim, ja
saskaitīsim zilacainu meitenīšu skaitu tūkstoš
jaundzimušo bērnu vidū Latvijas Republikā.
Apzīmējot šo skaitu ar m un dalot ar 1000, iegūsim
zilacaino meiteņu piedzimšanas biežumu 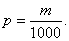 Šo p vērtību varam
uzlūkot par samērā precīzu zilacainas meitenītes
piedzimšanas varbūtību.
Šo p vērtību varam
uzlūkot par samērā precīzu zilacainas meitenītes
piedzimšanas varbūtību.
Subjektīvās
varbūtības jēgu varam ilustrēt ar nelielu sadzīvisku
sižetu. Varam iedomāties, ka ģimene apspriež dēla
iespējas iekļūt prestižā augstskolā. Jauneklis
vecākiem apgalvo: - Savas izredzes es vērtēju kā 7/10. -
Tēvs ir noskaņots kritiski un saka: - Man šķiet, ka tu
savas iespējas pārvērtē. Īstenībā tavas
izredzes ir vērtējamas kā 4/10, bet mēģināt tu
vari. - Māte neziņā svārstās, kuru no abiem
vērtējumiem atzīt par ticamāku dēla vai tēva.
Beidzot viņa nospriež, ka abi vērtējumi ir vienlīdz
ticami. Tas nozīmē, ka viņa katram no tiem piedēvē
ticamības varbūtību ½. Viegli saprast, ka mūsu
mazajā piemērā varbūtību skaitliskās
vērtības 7/10, 4/10 un ½ nav interpretējamas kā
izmēģinājuma sērijā iegūto rezultātu
biežumi. Šie skaitļi interpretējami kā attiecīgo
personu subjektīvās pārliecības pakāpes
kvantitatīvie novērtējumi.
Atgriežoties pie piemēra ar metamo
kauliņu, varam formulēt pirmo varbūtiskās loģikas
pamatprincipu P1. Saskaņā ar šo principu
aprēķināma dotajam notikumam A pretēja notikuma Ac
varbūtība. Piemēram, ja A ir notikums uzkrist sešām
acīm, tad šī notikuma varbūtība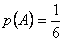 , bet notikuma Ac
varbūtība
, bet notikuma Ac
varbūtība 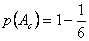 .
Vispārīgā veidā princips P1 izsakāms ar
formulu:
.
Vispārīgā veidā princips P1 izsakāms ar
formulu:
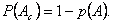
Ļoti svarīgs varbūtiskās
loģikas princips ir P2, kurš formulējams
šādi: ja viendabīga izmēģinājuma sērija
apmierina nosacījumu, ka iepriekšējo izmēģinājumu
rezultāti neietekmē nākošo izmēģinājumu
rezultātus, tad konkrētas rezultātu sērijas
parādīšanās varbūtība ir atsevišķo
rezultātu varbūtību reizinājums. Piemēram, ja
spēļu kauliņu metam 5 reizes, tad iespējamas 6*6*6*6*6 =
7776 dažādas rezultātu sērijas. Tā kā
atsevišķo metienu rezultāti cits citu neietekmē, tad
rezultātu sērijas 3,1,5,2,6 parādīšanās
varbūtība būs atsevišķo rezultātu
varbūtību reizinājums. Šajā gadījumā
dabūsim skaitli 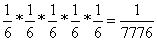 .
.
Trešais
varbūtiskās loģikas princips P3 formulējams
šādi: ja pazīme, kas nosaka notikuma A realizāciju, nav
savienojama ar pazīmi, kas nosaka notikuma B iestāšanos, tad
varbūtība, ka iestāsies vismaz viens no šiem notikumiem (A
vai B), ir atsevišķo notikumu varbūtību summa. Ar formulu
to pieraksta šādi:
p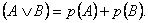
Principu P3 sauc par nesavienojamu
notikumu varbūtības saskaitīšanas likumu. Piemēram, ja
notikums A nozīmē uzmest spēļu kauliņu ar trim
acīm, bet notikums B uzmest kauliņu ar piecām acīm, A un
B būs nesavienojami notikumi, t. i., tie nevar realizēties reizē
vienā spēļu kauliņa metienā. Tātad
varbūtība vienā metienā iegūt A vai B ir 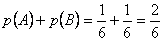 .
.
Šo triju varbūtiskās loģikas
principu lietojums ļauj aprēķināt daudzu un
dažādu notikumu un parādību varbūtības,
balstoties uz ļoti vienkāršu un elementāru notikumu
varbūtībām. Ar to palīdzību iespējams
kvalificēti analizēt kropļojumu parādības sakaru
kanālos, veikt ģenētisko parādību analīzi
bioloģijā, izvērtēt azartspēļu un loteriju
norises, veikt ražojumu kvalitātes statistiskās kontroles
rezultātu analīzi un medicīnisko preparātu efektivitātes
testēšanu. Arī kļūdu koriģējošu un
detektējošu kodu konstrukcija balstāma uz šo triju
varbūtiskās loģikas principu izmantošanu sakaru kanālu
trokšņu ietekmes matemātiskā modeļa, t. i.,
matemātiskā apraksta izveidē.
Informācijas pārraide un
varbūtiskā loģika
Ja sakaru kanālā
informācija tiek pārraidīta kā nuļļu un
vieninieku virknes, kurām atbilst noteikti elektronisko potenciālu
līmeņi, bet pastāv varbūtība p, ka
kārtējā bita pārraide dos kropļojumu 0
pārvērtīsies par 1, bet 1 par nulli, tad nereti lieto
kļūdu koriģējošus kodus, kuri pazemina
informācijas pārraides ātrumu, bet palielina tās
drošumu. Tā, piemēram, lai pārraidītu simbolu 0,
pārraidām koda vārdu 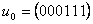 , bet 1 pārraidīšanai
izmantojam koda vārdu
, bet 1 pārraidīšanai
izmantojam koda vārdu 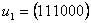 . Augsta informācijas pārraides
drošuma problēma ir ļoti aktuāla kosmisko sakaru sistēmās,
it īpaši sakaros starp kosmiskām zondēm un to vadības
centriem. Milzīgo attālumu dēļ un kosmiskās vides agresīvās
iedarbības rezultātā pārraidīto signālu
kropļojumi var parādīties ar pietiekami lielu
varbūtību, lai tos nevarētu ignorēt. Ja koda
vārdā
. Augsta informācijas pārraides
drošuma problēma ir ļoti aktuāla kosmisko sakaru sistēmās,
it īpaši sakaros starp kosmiskām zondēm un to vadības
centriem. Milzīgo attālumu dēļ un kosmiskās vides agresīvās
iedarbības rezultātā pārraidīto signālu
kropļojumi var parādīties ar pietiekami lielu
varbūtību, lai tos nevarētu ignorēt. Ja koda
vārdā 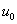 tiek
kropļota tikai viena pozīcija, tad iespējami šādi
seši varianti:
tiek
kropļota tikai viena pozīcija, tad iespējami šādi
seši varianti: 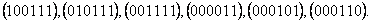 Citus
sešus variantus iegūsim, pārraidot koda vārdu
Citus
sešus variantus iegūsim, pārraidot koda vārdu 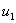 . Šajā
gadījumā iespējamie varianti ir:
. Šajā
gadījumā iespējamie varianti ir: 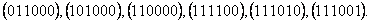 Saskaņā ar varbūtiskās
loģikas principiem
Saskaņā ar varbūtiskās
loģikas principiem 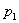 un
un 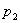 katra varianta
parādīšanās varbūtība izteiksies kā
reizinājums:
katra varianta
parādīšanās varbūtība izteiksies kā
reizinājums:
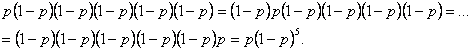
Varbūtiskās loģikas
principa p2 lietojums balstās uz atzinumu, ka
katras atsevišķas pozīcijas kropļojums, respektīvi,
nekropļojums nav atkarīgs no citu pozīciju stāvokļa.
Tā kā katra atsevišķa varianta realizācija
izslēdz cita varianta realizāciju, tad varbūtība, ka
iegūsim koda vārdu ar vienu vienīgu kropļojumu būs 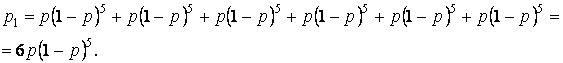 Varbūtība, ka,
pārraidot koda vārdu, tajā būs ne vairāk kā viens
kropļojums, izteiksies (saskaņā ar principu
Varbūtība, ka,
pārraidot koda vārdu, tajā būs ne vairāk kā viens
kropļojums, izteiksies (saskaņā ar principu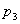 ) kā summa
) kā summa 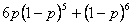 . Analoģiski tam,
kā aprēķinājām viena kropļojuma
iespējamību koda vārdā, varam izskaitļot
varbūtību,
. Analoģiski tam,
kā aprēķinājām viena kropļojuma
iespējamību koda vārdā, varam izskaitļot
varbūtību, 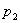 ,
ka pārraidītajā koda vārdā būs tieši divi
kropļojumi, dabūsim
,
ka pārraidītajā koda vārdā būs tieši divi
kropļojumi, dabūsim 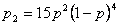 ,jo divi kropļojumi koda
vārdā dod 15 variantus. Tātad varbūtība p*, ka
kropļojumu skaits koda vārdā nepārsniedz divi, izteiksies
ar vienādību:
,jo divi kropļojumi koda
vārdā dod 15 variantus. Tātad varbūtība p*, ka
kropļojumu skaits koda vārdā nepārsniedz divi, izteiksies
ar vienādību:
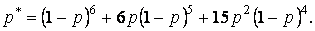
Atzīmēsim, ka šī
vienādība paliek spēkā arī tad, ja attiecīgā
bita kropļojums nevis pārveido 0 par 1 un 1 par 0, bet
transformē attiecīgo bitu par neidentificējamu signālu.
Viegli pārliecināties, ka koda vārds ar vienu vai diviem
kropļojumiem pieļauj identificēt sūtīto
oriģinālu, t. i., koda vārdu 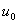 vai
vai 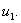 Tātad mūsu
izvēlētā kodēšanas metode ļauj koriģēt
līdz par diviem kropļojumiem koda vārdā. Ja šis
līmenis tiek pārsniegts, sūtītais koda vārds vairs nav
droši identificējams. Līdz ar to informācijas kanāla
drošuma rādītājs būs varbūtība
Tātad mūsu
izvēlētā kodēšanas metode ļauj koriģēt
līdz par diviem kropļojumiem koda vārdā. Ja šis
līmenis tiek pārsniegts, sūtītais koda vārds vairs nav
droši identificējams. Līdz ar to informācijas kanāla
drošuma rādītājs būs varbūtība 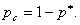
Aprēķināsim, cik lielu
drošuma palielinājumu dod mūsu kodēšanas metode, t.
i., cik mazu 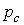 vērtību
iegūsim, ja p = 0,0001. Izrādās, ka šajā
gadījumā
vērtību
iegūsim, ja p = 0,0001. Izrādās, ka šajā
gadījumā 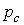 mazāks
par
mazāks
par 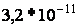 .
Tātad
.
Tātad 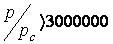 ,
t. i., informācijas pārraides drošums, palielinās
vairāk nekā 3000 000 reižu.
,
t. i., informācijas pārraides drošums, palielinās
vairāk nekā 3000 000 reižu.
Varbūtiskā loģika
un medicīna
Ar ļoti delikātām
varbūtiskās loģikas problēmām sastopamies
medicīnā. Jaunu zāļu un jaunu ārstniecības
metožu (it īpaši ķirurģisku) ieviešana ir
ļoti sarežģīts un atbildīgs process, kurā
nozīmīgu vietu ieņem statistisku datu vākšana un
izvērtēšana par labvēlīgo, respektīvi,
nelabvēlīgo gadījumu skaitu. Ilustrēsim šo
situāciju ar nelielu piemēru. Pieņemsim, ka jauna
medicīniska preparāta lietojums 75 gadījumos no 100 devis
pozitīvu rezultātu (pacienta veselības stāvoklis
būtiski uzlabojies), bet 25 gadījumos vai nu nedeva nekādus
veselības stāvokļa uzlabojumus, vai arī noveda pie
ļoti nevēlamām blaknēm. Rodas jautājums, kādus
secinājumus zāļu ražotāji un mediķi var izdarīt
no šādiem datiem. Vai varam teikt, ka šo zāļu
lietojums ar varbūtību p = 0,75 dod pozitīvu efektu?
Saskaņā ar varbūtiskās loģikas principiem P1,
P2, P3 varam apgalvot tikai to, ka paticamākā p
vērtība ir 0,75. Pievēršam lasītāju uzmanību
terminam paticamākā vērtība. Tā tiek
aprēķināta, lietojot t. s. maksimālās paticamības
metodi (ang. Maximum liklehood method), t. i., aprēķina p
vērtību, kura maksimizē aprakstītās statistiskās
situācijas rezultāta varbūtību, proti, dod maksimumu
izteiksmei
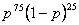 .
.
Lietojot samērā
sarežģītu varbūtiskās loģikas slēdzienu
ķēdi, varam secināt, ka patiesā p vērtība
no 0,75 var atšķirties par lielumu, kas mazāks vai vienāds
par 0,05. Varbūtība p vērtībai atrasties
robežās starp 0,70 un 0,80 ir apmēram vienāda 0,68.
Tātad varbūtība, ka patiesā p vērtība
būs mazāka par 0,70 vai lielāka par 0,80, ir pietiekami liela,
lai ar to rēķinātos. Mūs tomēr visvairāk
interesē varbūtība, ka patiesā p vērtība
ir mazāka par 0,60. Izrādās, ka zāļu
izmēģinājumā iegūtie rezultāti šādas
novirzes iespējamību garantē ar varbūtību, kas
mazāka par 0,0023. Tātad šāda novirze uzskatāma par
maz ticamu.
Runājot sadzīviskā
terminoloģijā, varam teikt, ka zāļu pozitīvais efekts
droši garantējams ne mazāk kā 60 procentiem pacientu.
Taču tūlīt rodas jautājums, ko šis skaitlis izsaka
pacientam, kuram ārsts rekomendē šīs zāles
iegādāties un lietot? Atbilde ir nedaudz pārsteidzoša.
Jebkuram konkrētam pacientam šie 60 procenti (ja vēlaties visi
75) neizsaka neko objektīvu, neko tādu, ko varētu svērt vai
mērīt pirms šo zāļu lietošanas. Šim skaitlim
ir un būs subjektīvas varbūtības jeb individuālas
pārliecības rādītāja loma, kas kvantitatīvi
atspoguļo indivīda noskaņojumu sagaidīt labvēlīgu
rezultātu, jo šis rādītājs tuvāks skaitlim 1, jo
lielāka iespēja tam izpausties pacienta (un arī ārsta)
pārliecībā, ka zāļu lietošana dos pozitīvu
efektu. Taču nav nekādas garantijas, ka no 100 jauniem pacientiem,
kuri šīs zāles lietos, mūsu konkrētais pacients
nebūs starp tiem 25 vai 40 indivīdiem, kuri pozitīvo ietekmi
negūs. Jāatzīmē arī šāds fakts. Ja
ārsts informē pacientu, ka konkrēta medicīniskā
preparāta lietojums nedod pozitīvu efektu tikai vienā
gadījumā no 1000 izmēģinājumiem, konkrētā
pacienta pārliecība par zāļu pozitīvo iedarbību
var izpausties placebo efekta veidā, t. i., tās var dot vēlamo
efektu pat tad, ja farmakoloģiskā iedarbība tām būtu
līdzvērtīga nullei.
Varbūtiskā loģika
un rīcības motivācija
Lai gan varbūtības p lielums kalpo
par motivāciju praktiskai rīcībai, tomēr pastāv
neatbilstība starp p vērtību un indivīda
pieņemto lēmumu. Mūsu piemērā pacients būs
vairāk noskaņots zāles iegādāties un lietot, jo
tuvāk 1 būs ārsta nosauktā p vērtība.
Citos gadījumos indivīds var pieņemt lēmumu attiecīgi
rīkoties arī tad, ja varbūtība p realizēties
viņu interesējošam notikumam nav sevišķi liela. Nav
pamata apgalvot, ka varbūtība pakļūt zem
automašīnas riteņiem ir ļoti liela, ja
šķērsosiet ielu gar stāvoša pasažieru autobusa
priekšpusi; tās varbūtība iespējams nav lielāka
par 0,50, taču sekas šādam negadījumam būs
briesmīgas. Tādēļ labāk šādu soli nespert,
bet censties apiet autobusu gar tā aizmuguri.
Interesantu personas rīcības
motivāciju, kas balstīta uz notikuma varbūtības un
šī notikuma nozīmes ievērošanu, sniedz slavenais
franču matemātiķis un filozofs Blezs Paskāls (1623.1662.)
filozofiskajā darbā Domas (franciski - pensées).
Vienā no šī sacerējuma esejām viņš sniedz
motivāciju, kādēļ skeptiski noskaņotam cilvēkam
būtu pamats ticēt Dieva esamībai. Viņa argumentācijas
būtība ir šāda: varbūtība, ka Dievs eksistē,
ir maza (pēc skeptiķu domām), bet ticība Dieva eksistencei
garantē bezgalīgu svētlaimi, ja viņš
patiešām eksistē. Turpretī neticība Dieva
esamībai nolemj cilvēku mūžīgām
ciešanām, ja Dievs tomēr eksistē. Ja Dieva tomēr nav,
ticība viņam būs saistīta tikai ar nelieliem
zaudējumiem. Tātad arī skeptiķim pēc B. Paskāla
domām ieteicams kļūt ticīgam.
Šo
pašu ticības jautājumu no varbūtiskās loģikas
viedokļa iztirzājis slavenais B. Paskāla tautietis franču
matemātiķis Pjērs Laplass (1749.1827.). Viņš
centās atspēkot Paskāla argumentāciju, balstoties uz
šādu tēzi: jo vairāk kāds sola, jo mazāk tam var
ticēt. Ja mums sola bezgalīgu svētlaimi, tad
varbūtība, ka tā tiks garantēta, ir bezgalīgi maza.
Pievēršam lasītāja uzmanību faktam, ka abi franču
domātāji spriedumos operē ar subjektīvās, nevis
objektīvās varbūtības jēdzienu. Bet, tā kā
viņi iztirzā personas rīcības motivāciju, kas
izpaudīsies vienā konkrētā lēmumā, tad
varbūtības objektivitātei šeit nav nozīmes.
Varbūtiskās loģikas
slēdzienu kļūdas
Visizplatītākā varbūtiskās
loģikas slēdzienu kļūda ir saistīta ar varbūtisko
izteikumu interpretāciju. Piemēram, balstoties uz loģikas
principu  ,
matemātiķi var aprēķināt varbūtību, ka,
vienlaikus metot 10 spēļu kauliņus, mēs uzmetīsim 10
sešiniekus. Ja spēļu kauliņi nav viltoti, tad šī
notikuma varbūtība
,
matemātiķi var aprēķināt varbūtību, ka,
vienlaikus metot 10 spēļu kauliņus, mēs uzmetīsim 10
sešiniekus. Ja spēļu kauliņi nav viltoti, tad šī
notikuma varbūtība 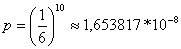 . Neprofesionālis šo
rezultātu var pasniegt plašākai sabiedrībai saprotamā
formā un sacīt: - Lai vienu reizi iegūtu 10 sešiniekus,
jāizdara vismaz 165 miljoni metienu. - Nereti tiek lietota arī
šāda interpretācija: 10 sešiniekus iegūsim tikai
vienā gadījumā no 165 miljoniem.
. Neprofesionālis šo
rezultātu var pasniegt plašākai sabiedrībai saprotamā
formā un sacīt: - Lai vienu reizi iegūtu 10 sešiniekus,
jāizdara vismaz 165 miljoni metienu. - Nereti tiek lietota arī
šāda interpretācija: 10 sešiniekus iegūsim tikai
vienā gadījumā no 165 miljoniem.
Līdzīga varbūtiskās
loģikas kļūda tika pieļauta gan ārzemju, gan mūsu
valsts plašsaziņas līdzekļos 25. un 26. augustā.
Atgādinām lasītājam, ka 24. augustā pasauli
pāršalca ziņa, ka gandrīz vienlaikus avarējušas
divas Krievijas pasažieru lidmašīnas. Tika izteiktas aizdomas
par iespējamu terora aktu, kuru sākotnēji Krievijas
drošības orgānu pārstāvji noliedza. Tad vācu
raidstacija Deutche Welle nāca klajā ar paziņojumu, ka
matemātiķi aprēķinājuši lidmašīnu
vienlaikus avārijas gadījumrakstura iespējamību un
secinājuši, ka tā var realizēties vienu reizi piecos
tūkstošos gadu. Pēc tam to atkārtoja Latvijas Radio 1.
Šāds formulējums žurnālistu priekšnesumā
varēja parādīties pie nosacījuma, ka matemātiķu
aprēķinos vienlaikus avārijas varbūtība viena gada
laikā nav lielāka par 1/5000. Lai arī cik apšaubāms
būtu šāds matemātiķu aprēķins, pats
apgalvojums, ka šāda avārija var notikt tikai reizi 5000 gados,
ir tīrais blefs. Ja aprēķinātā varbūtība ir
pareiza, tad patiesais avāriju skaits 5000 gadu laikā var būt
arī lielāks par vienu. Izmantojot varbūtiskās loģikas
principus P1, P2 un P3, viegli
aprēķināt šāda notikuma varbūtību.
Izrādās, ka vairāk par vienu gadījumrakstura vienlaikus
avāriju 5000 gados varam sagaidīt ar varbūtību, kas
lielāka par ¼.
Varbūtiskā loģika
ir pilnīgi nepieciešama, ja vēlamies iztirzāt
demogrāfiskās un ģenētiskās parādības.
Austriešu mūks Gregors Mendelis (1822.1884.), kurš atklāja
pirmos ģenētikas pamatlikumus, tos varēja formulēt
vienīgi kā statistiskus jeb varbūtiskus likumus. Viens no G.
Mendeļa atklātajiem ģenētikas likumiem formulējams
šādi: biežums, ar kādu dominantā pazīme sastopama
otrajā hibrīdu paaudzē, ir tuvs lielumam 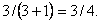 Varbūtību valodā
tas nozīmē, lūk, ko: pēc Mendeļa varbūtība,
ka otrajā hibrīdu paaudzē parādīsies indivīds ar
dominanto pazīmi, ir ¾.
Varbūtību valodā
tas nozīmē, lūk, ko: pēc Mendeļa varbūtība,
ka otrajā hibrīdu paaudzē parādīsies indivīds ar
dominanto pazīmi, ir ¾.
Ļoti delikāts ir
jautājums par šādu un tamlīdzīgu statistisku likumu
pārbaudi. Tā kā varbūtība objektīvi
manifestējas kā parādības biežums samērā
lielā izmēģinājumu sērijā, kas tikai retos
gadījumos sakrīt ar likumā uzrādīto
varbūtību, tad pastāv iespēja apstrīdēt
formulētā likuma pareizību. Ar G. Mendeļa formulēto
ģenētikas likumu tieši tā arī notika. T. Lisenko
skolniece N. Jermolajeva veica plašus eksperimentus un, balstoties uz
iegūtā biežuma nesakritību ar varbūtību ¾,
apšaubīja Mendeļa likuma pareizību. Viņas
pieļautā kļūda izskaidrojama ar to, kā 1939. gada
publikācijā viņa neprofesionāli novērtēja
iegūtā biežuma atšķirību no varbūtības
¾. Šo kļūdu pamanīja ievērojamais krievu
matemātiķis A. Kolmogorovs (1903.-1987.).
Profesors Aivars LORENCS
Varbūtiskajā loģikā mūsu slēdzieni saistīti ar spriedumiem, kuros atklāti vai apslēpti figurē varbūtības termins. Šāda tipa sprieduma piemērs ir apgalvojums, ka spēļu kauliņa noteiktas skaldnes uzkrišanas varbūtība ir 1/6. Šai kategorijai pieder arī apgalvojums varbūtība, ka jaunas ģimenes pirmdzimtais būs zēns ir ½.
Svarīgi atzīmēt, ka
pastāv būtiska atšķirība starp varbūtības
jēdziena saturu, ar kuru operējam sadzīvē, un šī
termina semantiku tehnikā un dabas zinātnēs. Pirmajā
gadījumā mums ir darīšana ar t. s. subjektīvo
varbūtību, otrajā - ar objektīvo. Zēna vai meitenes
piedzimšana pieskaitāma objektīvo varbūtību
kategorijai un interpretējama kā attiecīgās
parādības novērojamais biežums samērā lielā
izmēģinājuma skaitā. Tā, piemēram, ja uz labu
laimi izvēlēsimies tūkstoš ģimeņu, tad zēnu
un meiteņu skaita attiecība pirmdzimto vidū būs ļoti
tuva 500/500. Pavisam citu statistisko biežumu iegūsim, ja
saskaitīsim zilacainu meitenīšu skaitu tūkstoš
jaundzimušo bērnu vidū Latvijas Republikā.
Apzīmējot šo skaitu ar m un dalot ar 1000, iegūsim
zilacaino meiteņu piedzimšanas biežumu ![]() Šo p vērtību varam
uzlūkot par samērā precīzu zilacainas meitenītes
piedzimšanas varbūtību.
Šo p vērtību varam
uzlūkot par samērā precīzu zilacainas meitenītes
piedzimšanas varbūtību.
Subjektīvās varbūtības jēgu varam ilustrēt ar nelielu sadzīvisku sižetu. Varam iedomāties, ka ģimene apspriež dēla iespējas iekļūt prestižā augstskolā. Jauneklis vecākiem apgalvo: - Savas izredzes es vērtēju kā 7/10. - Tēvs ir noskaņots kritiski un saka: - Man šķiet, ka tu savas iespējas pārvērtē. Īstenībā tavas izredzes ir vērtējamas kā 4/10, bet mēģināt tu vari. - Māte neziņā svārstās, kuru no abiem vērtējumiem atzīt par ticamāku dēla vai tēva. Beidzot viņa nospriež, ka abi vērtējumi ir vienlīdz ticami. Tas nozīmē, ka viņa katram no tiem piedēvē ticamības varbūtību ½. Viegli saprast, ka mūsu mazajā piemērā varbūtību skaitliskās vērtības 7/10, 4/10 un ½ nav interpretējamas kā izmēģinājuma sērijā iegūto rezultātu biežumi. Šie skaitļi interpretējami kā attiecīgo personu subjektīvās pārliecības pakāpes kvantitatīvie novērtējumi.
Atgriežoties pie piemēra ar metamo
kauliņu, varam formulēt pirmo varbūtiskās loģikas
pamatprincipu P1. Saskaņā ar šo principu
aprēķināma dotajam notikumam A pretēja notikuma Ac
varbūtība. Piemēram, ja A ir notikums uzkrist sešām
acīm, tad šī notikuma varbūtība![]() , bet notikuma Ac
varbūtība
, bet notikuma Ac
varbūtība ![]() .
Vispārīgā veidā princips P1 izsakāms ar
formulu:
.
Vispārīgā veidā princips P1 izsakāms ar
formulu:
![]()
Ļoti svarīgs varbūtiskās
loģikas princips ir P2, kurš formulējams
šādi: ja viendabīga izmēģinājuma sērija
apmierina nosacījumu, ka iepriekšējo izmēģinājumu
rezultāti neietekmē nākošo izmēģinājumu
rezultātus, tad konkrētas rezultātu sērijas
parādīšanās varbūtība ir atsevišķo
rezultātu varbūtību reizinājums. Piemēram, ja
spēļu kauliņu metam 5 reizes, tad iespējamas 6*6*6*6*6 =
7776 dažādas rezultātu sērijas. Tā kā
atsevišķo metienu rezultāti cits citu neietekmē, tad
rezultātu sērijas 3,1,5,2,6 parādīšanās
varbūtība būs atsevišķo rezultātu
varbūtību reizinājums. Šajā gadījumā
dabūsim skaitli ![]() .
.
Trešais varbūtiskās loģikas princips P3 formulējams šādi: ja pazīme, kas nosaka notikuma A realizāciju, nav savienojama ar pazīmi, kas nosaka notikuma B iestāšanos, tad varbūtība, ka iestāsies vismaz viens no šiem notikumiem (A vai B), ir atsevišķo notikumu varbūtību summa. Ar formulu to pieraksta šādi:
p![]()
Principu P3 sauc par nesavienojamu
notikumu varbūtības saskaitīšanas likumu. Piemēram, ja
notikums A nozīmē uzmest spēļu kauliņu ar trim
acīm, bet notikums B uzmest kauliņu ar piecām acīm, A un
B būs nesavienojami notikumi, t. i., tie nevar realizēties reizē
vienā spēļu kauliņa metienā. Tātad
varbūtība vienā metienā iegūt A vai B ir ![]() .
.
Šo triju varbūtiskās loģikas principu lietojums ļauj aprēķināt daudzu un dažādu notikumu un parādību varbūtības, balstoties uz ļoti vienkāršu un elementāru notikumu varbūtībām. Ar to palīdzību iespējams kvalificēti analizēt kropļojumu parādības sakaru kanālos, veikt ģenētisko parādību analīzi bioloģijā, izvērtēt azartspēļu un loteriju norises, veikt ražojumu kvalitātes statistiskās kontroles rezultātu analīzi un medicīnisko preparātu efektivitātes testēšanu. Arī kļūdu koriģējošu un detektējošu kodu konstrukcija balstāma uz šo triju varbūtiskās loģikas principu izmantošanu sakaru kanālu trokšņu ietekmes matemātiskā modeļa, t. i., matemātiskā apraksta izveidē.
Informācijas pārraide un varbūtiskā loģika
Ja sakaru kanālā
informācija tiek pārraidīta kā nuļļu un
vieninieku virknes, kurām atbilst noteikti elektronisko potenciālu
līmeņi, bet pastāv varbūtība p, ka
kārtējā bita pārraide dos kropļojumu 0
pārvērtīsies par 1, bet 1 par nulli, tad nereti lieto
kļūdu koriģējošus kodus, kuri pazemina
informācijas pārraides ātrumu, bet palielina tās
drošumu. Tā, piemēram, lai pārraidītu simbolu 0,
pārraidām koda vārdu ![]() , bet 1 pārraidīšanai
izmantojam koda vārdu
, bet 1 pārraidīšanai
izmantojam koda vārdu ![]() . Augsta informācijas pārraides
drošuma problēma ir ļoti aktuāla kosmisko sakaru sistēmās,
it īpaši sakaros starp kosmiskām zondēm un to vadības
centriem. Milzīgo attālumu dēļ un kosmiskās vides agresīvās
iedarbības rezultātā pārraidīto signālu
kropļojumi var parādīties ar pietiekami lielu
varbūtību, lai tos nevarētu ignorēt. Ja koda
vārdā
. Augsta informācijas pārraides
drošuma problēma ir ļoti aktuāla kosmisko sakaru sistēmās,
it īpaši sakaros starp kosmiskām zondēm un to vadības
centriem. Milzīgo attālumu dēļ un kosmiskās vides agresīvās
iedarbības rezultātā pārraidīto signālu
kropļojumi var parādīties ar pietiekami lielu
varbūtību, lai tos nevarētu ignorēt. Ja koda
vārdā ![]() tiek
kropļota tikai viena pozīcija, tad iespējami šādi
seši varianti:
tiek
kropļota tikai viena pozīcija, tad iespējami šādi
seši varianti: ![]() Citus
sešus variantus iegūsim, pārraidot koda vārdu
Citus
sešus variantus iegūsim, pārraidot koda vārdu ![]() . Šajā
gadījumā iespējamie varianti ir:
. Šajā
gadījumā iespējamie varianti ir: ![]() Saskaņā ar varbūtiskās
loģikas principiem
Saskaņā ar varbūtiskās
loģikas principiem ![]() un
un ![]() katra varianta
parādīšanās varbūtība izteiksies kā
reizinājums:
katra varianta
parādīšanās varbūtība izteiksies kā
reizinājums:
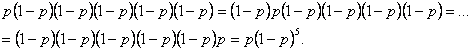
Varbūtiskās loģikas
principa p2 lietojums balstās uz atzinumu, ka
katras atsevišķas pozīcijas kropļojums, respektīvi,
nekropļojums nav atkarīgs no citu pozīciju stāvokļa.
Tā kā katra atsevišķa varianta realizācija
izslēdz cita varianta realizāciju, tad varbūtība, ka
iegūsim koda vārdu ar vienu vienīgu kropļojumu būs 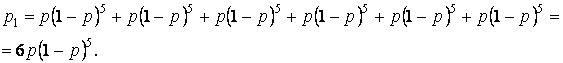 Varbūtība, ka,
pārraidot koda vārdu, tajā būs ne vairāk kā viens
kropļojums, izteiksies (saskaņā ar principu
Varbūtība, ka,
pārraidot koda vārdu, tajā būs ne vairāk kā viens
kropļojums, izteiksies (saskaņā ar principu![]() ) kā summa
) kā summa ![]() . Analoģiski tam,
kā aprēķinājām viena kropļojuma
iespējamību koda vārdā, varam izskaitļot
varbūtību,
. Analoģiski tam,
kā aprēķinājām viena kropļojuma
iespējamību koda vārdā, varam izskaitļot
varbūtību, ![]() ,
ka pārraidītajā koda vārdā būs tieši divi
kropļojumi, dabūsim
,
ka pārraidītajā koda vārdā būs tieši divi
kropļojumi, dabūsim ![]() ,jo divi kropļojumi koda
vārdā dod 15 variantus. Tātad varbūtība p*, ka
kropļojumu skaits koda vārdā nepārsniedz divi, izteiksies
ar vienādību:
,jo divi kropļojumi koda
vārdā dod 15 variantus. Tātad varbūtība p*, ka
kropļojumu skaits koda vārdā nepārsniedz divi, izteiksies
ar vienādību:
![]()
Atzīmēsim, ka šī
vienādība paliek spēkā arī tad, ja attiecīgā
bita kropļojums nevis pārveido 0 par 1 un 1 par 0, bet
transformē attiecīgo bitu par neidentificējamu signālu.
Viegli pārliecināties, ka koda vārds ar vienu vai diviem
kropļojumiem pieļauj identificēt sūtīto
oriģinālu, t. i., koda vārdu ![]() vai
vai ![]() Tātad mūsu
izvēlētā kodēšanas metode ļauj koriģēt
līdz par diviem kropļojumiem koda vārdā. Ja šis
līmenis tiek pārsniegts, sūtītais koda vārds vairs nav
droši identificējams. Līdz ar to informācijas kanāla
drošuma rādītājs būs varbūtība
Tātad mūsu
izvēlētā kodēšanas metode ļauj koriģēt
līdz par diviem kropļojumiem koda vārdā. Ja šis
līmenis tiek pārsniegts, sūtītais koda vārds vairs nav
droši identificējams. Līdz ar to informācijas kanāla
drošuma rādītājs būs varbūtība ![]()
Aprēķināsim, cik lielu
drošuma palielinājumu dod mūsu kodēšanas metode, t.
i., cik mazu ![]() vērtību
iegūsim, ja p = 0,0001. Izrādās, ka šajā
gadījumā
vērtību
iegūsim, ja p = 0,0001. Izrādās, ka šajā
gadījumā ![]() mazāks
par
mazāks
par ![]() .
Tātad
.
Tātad ![]() ,
t. i., informācijas pārraides drošums, palielinās
vairāk nekā 3000 000 reižu.
,
t. i., informācijas pārraides drošums, palielinās
vairāk nekā 3000 000 reižu.
Varbūtiskā loģika un medicīna
Ar ļoti delikātām varbūtiskās loģikas problēmām sastopamies medicīnā. Jaunu zāļu un jaunu ārstniecības metožu (it īpaši ķirurģisku) ieviešana ir ļoti sarežģīts un atbildīgs process, kurā nozīmīgu vietu ieņem statistisku datu vākšana un izvērtēšana par labvēlīgo, respektīvi, nelabvēlīgo gadījumu skaitu. Ilustrēsim šo situāciju ar nelielu piemēru. Pieņemsim, ka jauna medicīniska preparāta lietojums 75 gadījumos no 100 devis pozitīvu rezultātu (pacienta veselības stāvoklis būtiski uzlabojies), bet 25 gadījumos vai nu nedeva nekādus veselības stāvokļa uzlabojumus, vai arī noveda pie ļoti nevēlamām blaknēm. Rodas jautājums, kādus secinājumus zāļu ražotāji un mediķi var izdarīt no šādiem datiem. Vai varam teikt, ka šo zāļu lietojums ar varbūtību p = 0,75 dod pozitīvu efektu? Saskaņā ar varbūtiskās loģikas principiem P1, P2, P3 varam apgalvot tikai to, ka paticamākā p vērtība ir 0,75. Pievēršam lasītāju uzmanību terminam paticamākā vērtība. Tā tiek aprēķināta, lietojot t. s. maksimālās paticamības metodi (ang. Maximum liklehood method), t. i., aprēķina p vērtību, kura maksimizē aprakstītās statistiskās situācijas rezultāta varbūtību, proti, dod maksimumu izteiksmei
![]() .
.
Lietojot samērā sarežģītu varbūtiskās loģikas slēdzienu ķēdi, varam secināt, ka patiesā p vērtība no 0,75 var atšķirties par lielumu, kas mazāks vai vienāds par 0,05. Varbūtība p vērtībai atrasties robežās starp 0,70 un 0,80 ir apmēram vienāda 0,68. Tātad varbūtība, ka patiesā p vērtība būs mazāka par 0,70 vai lielāka par 0,80, ir pietiekami liela, lai ar to rēķinātos. Mūs tomēr visvairāk interesē varbūtība, ka patiesā p vērtība ir mazāka par 0,60. Izrādās, ka zāļu izmēģinājumā iegūtie rezultāti šādas novirzes iespējamību garantē ar varbūtību, kas mazāka par 0,0023. Tātad šāda novirze uzskatāma par maz ticamu.
Runājot sadzīviskā terminoloģijā, varam teikt, ka zāļu pozitīvais efekts droši garantējams ne mazāk kā 60 procentiem pacientu. Taču tūlīt rodas jautājums, ko šis skaitlis izsaka pacientam, kuram ārsts rekomendē šīs zāles iegādāties un lietot? Atbilde ir nedaudz pārsteidzoša. Jebkuram konkrētam pacientam šie 60 procenti (ja vēlaties visi 75) neizsaka neko objektīvu, neko tādu, ko varētu svērt vai mērīt pirms šo zāļu lietošanas. Šim skaitlim ir un būs subjektīvas varbūtības jeb individuālas pārliecības rādītāja loma, kas kvantitatīvi atspoguļo indivīda noskaņojumu sagaidīt labvēlīgu rezultātu, jo šis rādītājs tuvāks skaitlim 1, jo lielāka iespēja tam izpausties pacienta (un arī ārsta) pārliecībā, ka zāļu lietošana dos pozitīvu efektu. Taču nav nekādas garantijas, ka no 100 jauniem pacientiem, kuri šīs zāles lietos, mūsu konkrētais pacients nebūs starp tiem 25 vai 40 indivīdiem, kuri pozitīvo ietekmi negūs. Jāatzīmē arī šāds fakts. Ja ārsts informē pacientu, ka konkrēta medicīniskā preparāta lietojums nedod pozitīvu efektu tikai vienā gadījumā no 1000 izmēģinājumiem, konkrētā pacienta pārliecība par zāļu pozitīvo iedarbību var izpausties placebo efekta veidā, t. i., tās var dot vēlamo efektu pat tad, ja farmakoloģiskā iedarbība tām būtu līdzvērtīga nullei.
Varbūtiskā loģika un rīcības motivācija
Lai gan varbūtības p lielums kalpo par motivāciju praktiskai rīcībai, tomēr pastāv neatbilstība starp p vērtību un indivīda pieņemto lēmumu. Mūsu piemērā pacients būs vairāk noskaņots zāles iegādāties un lietot, jo tuvāk 1 būs ārsta nosauktā p vērtība. Citos gadījumos indivīds var pieņemt lēmumu attiecīgi rīkoties arī tad, ja varbūtība p realizēties viņu interesējošam notikumam nav sevišķi liela. Nav pamata apgalvot, ka varbūtība pakļūt zem automašīnas riteņiem ir ļoti liela, ja šķērsosiet ielu gar stāvoša pasažieru autobusa priekšpusi; tās varbūtība iespējams nav lielāka par 0,50, taču sekas šādam negadījumam būs briesmīgas. Tādēļ labāk šādu soli nespert, bet censties apiet autobusu gar tā aizmuguri.
Interesantu personas rīcības motivāciju, kas balstīta uz notikuma varbūtības un šī notikuma nozīmes ievērošanu, sniedz slavenais franču matemātiķis un filozofs Blezs Paskāls (1623.1662.) filozofiskajā darbā Domas (franciski - pensées). Vienā no šī sacerējuma esejām viņš sniedz motivāciju, kādēļ skeptiski noskaņotam cilvēkam būtu pamats ticēt Dieva esamībai. Viņa argumentācijas būtība ir šāda: varbūtība, ka Dievs eksistē, ir maza (pēc skeptiķu domām), bet ticība Dieva eksistencei garantē bezgalīgu svētlaimi, ja viņš patiešām eksistē. Turpretī neticība Dieva esamībai nolemj cilvēku mūžīgām ciešanām, ja Dievs tomēr eksistē. Ja Dieva tomēr nav, ticība viņam būs saistīta tikai ar nelieliem zaudējumiem. Tātad arī skeptiķim pēc B. Paskāla domām ieteicams kļūt ticīgam.
Šo pašu ticības jautājumu no varbūtiskās loģikas viedokļa iztirzājis slavenais B. Paskāla tautietis franču matemātiķis Pjērs Laplass (1749.1827.). Viņš centās atspēkot Paskāla argumentāciju, balstoties uz šādu tēzi: jo vairāk kāds sola, jo mazāk tam var ticēt. Ja mums sola bezgalīgu svētlaimi, tad varbūtība, ka tā tiks garantēta, ir bezgalīgi maza. Pievēršam lasītāja uzmanību faktam, ka abi franču domātāji spriedumos operē ar subjektīvās, nevis objektīvās varbūtības jēdzienu. Bet, tā kā viņi iztirzā personas rīcības motivāciju, kas izpaudīsies vienā konkrētā lēmumā, tad varbūtības objektivitātei šeit nav nozīmes.
Varbūtiskās loģikas slēdzienu kļūdas
Visizplatītākā varbūtiskās
loģikas slēdzienu kļūda ir saistīta ar varbūtisko
izteikumu interpretāciju. Piemēram, balstoties uz loģikas
principu ![]() ,
matemātiķi var aprēķināt varbūtību, ka,
vienlaikus metot 10 spēļu kauliņus, mēs uzmetīsim 10
sešiniekus. Ja spēļu kauliņi nav viltoti, tad šī
notikuma varbūtība
,
matemātiķi var aprēķināt varbūtību, ka,
vienlaikus metot 10 spēļu kauliņus, mēs uzmetīsim 10
sešiniekus. Ja spēļu kauliņi nav viltoti, tad šī
notikuma varbūtība ![]() . Neprofesionālis šo
rezultātu var pasniegt plašākai sabiedrībai saprotamā
formā un sacīt: - Lai vienu reizi iegūtu 10 sešiniekus,
jāizdara vismaz 165 miljoni metienu. - Nereti tiek lietota arī
šāda interpretācija: 10 sešiniekus iegūsim tikai
vienā gadījumā no 165 miljoniem.
. Neprofesionālis šo
rezultātu var pasniegt plašākai sabiedrībai saprotamā
formā un sacīt: - Lai vienu reizi iegūtu 10 sešiniekus,
jāizdara vismaz 165 miljoni metienu. - Nereti tiek lietota arī
šāda interpretācija: 10 sešiniekus iegūsim tikai
vienā gadījumā no 165 miljoniem.
Līdzīga varbūtiskās loģikas kļūda tika pieļauta gan ārzemju, gan mūsu valsts plašsaziņas līdzekļos 25. un 26. augustā. Atgādinām lasītājam, ka 24. augustā pasauli pāršalca ziņa, ka gandrīz vienlaikus avarējušas divas Krievijas pasažieru lidmašīnas. Tika izteiktas aizdomas par iespējamu terora aktu, kuru sākotnēji Krievijas drošības orgānu pārstāvji noliedza. Tad vācu raidstacija Deutche Welle nāca klajā ar paziņojumu, ka matemātiķi aprēķinājuši lidmašīnu vienlaikus avārijas gadījumrakstura iespējamību un secinājuši, ka tā var realizēties vienu reizi piecos tūkstošos gadu. Pēc tam to atkārtoja Latvijas Radio 1. Šāds formulējums žurnālistu priekšnesumā varēja parādīties pie nosacījuma, ka matemātiķu aprēķinos vienlaikus avārijas varbūtība viena gada laikā nav lielāka par 1/5000. Lai arī cik apšaubāms būtu šāds matemātiķu aprēķins, pats apgalvojums, ka šāda avārija var notikt tikai reizi 5000 gados, ir tīrais blefs. Ja aprēķinātā varbūtība ir pareiza, tad patiesais avāriju skaits 5000 gadu laikā var būt arī lielāks par vienu. Izmantojot varbūtiskās loģikas principus P1, P2 un P3, viegli aprēķināt šāda notikuma varbūtību. Izrādās, ka vairāk par vienu gadījumrakstura vienlaikus avāriju 5000 gados varam sagaidīt ar varbūtību, kas lielāka par ¼.
Varbūtiskā loģika
ir pilnīgi nepieciešama, ja vēlamies iztirzāt
demogrāfiskās un ģenētiskās parādības.
Austriešu mūks Gregors Mendelis (1822.1884.), kurš atklāja
pirmos ģenētikas pamatlikumus, tos varēja formulēt
vienīgi kā statistiskus jeb varbūtiskus likumus. Viens no G.
Mendeļa atklātajiem ģenētikas likumiem formulējams
šādi: biežums, ar kādu dominantā pazīme sastopama
otrajā hibrīdu paaudzē, ir tuvs lielumam ![]() Varbūtību valodā
tas nozīmē, lūk, ko: pēc Mendeļa varbūtība,
ka otrajā hibrīdu paaudzē parādīsies indivīds ar
dominanto pazīmi, ir ¾.
Varbūtību valodā
tas nozīmē, lūk, ko: pēc Mendeļa varbūtība,
ka otrajā hibrīdu paaudzē parādīsies indivīds ar
dominanto pazīmi, ir ¾.
Ļoti delikāts ir jautājums par šādu un tamlīdzīgu statistisku likumu pārbaudi. Tā kā varbūtība objektīvi manifestējas kā parādības biežums samērā lielā izmēģinājumu sērijā, kas tikai retos gadījumos sakrīt ar likumā uzrādīto varbūtību, tad pastāv iespēja apstrīdēt formulētā likuma pareizību. Ar G. Mendeļa formulēto ģenētikas likumu tieši tā arī notika. T. Lisenko skolniece N. Jermolajeva veica plašus eksperimentus un, balstoties uz iegūtā biežuma nesakritību ar varbūtību ¾, apšaubīja Mendeļa likuma pareizību. Viņas pieļautā kļūda izskaidrojama ar to, kā 1939. gada publikācijā viņa neprofesionāli novērtēja iegūtā biežuma atšķirību no varbūtības ¾. Šo kļūdu pamanīja ievērojamais krievu matemātiķis A. Kolmogorovs (1903.-1987.).
Profesors Aivars LORENCS

